ЕГЭ (базовый уровень) № 20 решаем сами за пять минут. В войсковой части 32103 имеется 3 вида салата 2 вида первого блюда

РЕШЕНИЯ ЗАДАЧ № 20 БАЗА егэ

РЕШЕНИЕ

Для полученных прямоугольников должно выполняться:

18*20=12*Х

Тогда Х=(18*20)/12=30

ОТВЕТ: 30

20. ТУДА-СЮДА

Улит­ка за день за­пол­за­ет вверх по де­ре­ву на А м, а за ночь спол­за­ет на В м. Вы­со­та де­ре­ва С м. За сколь­ко дней улит­ка впер­вые до­ползёт до вер­ши­ны де­ре­ва?

РЕШЕНИЕ

За одни сутки улитка может подняться на высоту (А-В) метров. Так как она за один день может подняться на высоту А, то до последнего подъема ей необходимо преодолеть высоту (С-А). Исходя из этого, получаем что она будет подниматься (С-А)\(А-В)+1 (единицу прибавляем так как она за один день поднимается на высоту А).

ПРИМЕР

Улит­ка за день за­пол­за­ет вверх по де­ре­ву на 4 м, а за ночь спол­за­ет на 3 м. Вы­со­та де­ре­ва 10 м. За сколь­ко дней улит­ка впер­вые до­ползёт до вер­ши­ны де­ре­ва?

РЕШЕНИЕ

Возвращаясь к нашим рассуждениям получаем

(10-4)/(4-3)+1=7

ОТВЕТ за 7 дней

Следует отметить что таким способ можно решать задачи на наполнение чего либо, когда поступает что-то и что-то вытекает.

21. ПРЫЖКИ ПО ПРЯМОЙ

Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав Х прыжков, начиная прыгать из начала координат?

РЕШЕНИЕ

Предположим, что кузнечик делает все прыжки в одну сторону, тогда он попадет в точку с координатой Х. Теперь он прыгает вперед на (Х-1) прыжков и один обратно: попадает в точку с координатой (Х-2). Рассматривая таким способом все его прыжки можно заметить, что он будет находиться в точках с координатами Х, (Х-2),(Х-4) и т.д. Данная зависимость является не чем иным как арифметической прогрессией с разностью d=-2 и а1=Х, а an=-X. Тогда количество членов этой прогрессии и есть количество точек в которых он может оказаться. Найдем их

an=a1+d(n-1)

-X=X+d(n-1)

-2X=-2(n-1)

n=X+1

ПРИМЕР

Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав 10 прыжков, начиная прыгать из начала координат?

РЕШЕНИЕ

Основываясь на выше приведенных выводах получаем

10+1=11

ОТВЕТ 11 точек

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

1. Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд ста­кан будет за­пол­нен бак­те­ри­я­ми на­по­ло­ви­ну?

2. На палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жёлтого и зелёного цвета. Если рас­пи­лить палку по крас­ным ли­ни­ям, по­лу­чит­ся 15 кус­ков, если по жёлтым — 5 кус­ков, а если по зелёным — 7 кус­ков. Сколь­ко кус­ков по­лу­чит­ся, если рас­пи­лить палку по ли­ни­ям всех трёх цве­тов?

3. Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за один пры­жок. Куз­не­чик на­чи­на­ет пры­гать из на­ча­ла ко­ор­ди­нат. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 11 прыж­ков?

4. В кор­зи­не лежит 40 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 17 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 25 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

5. Саша при­гла­сил Петю в гости, ска­зав, что живёт в седь­мом подъ­ез­де в квар­ти­ре № 462, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом се­ми­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

6. Саша при­гла­сил Петю в гости, ска­зав, что живёт в вось­мом подъ­ез­де в квар­ти­ре № 468, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом две­на­дца­ти­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

7. Саша при­гла­сил Петю в гости, ска­зав, что живёт в две­на­дца­том подъ­ез­де в квар­ти­ре № 465, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом пя­ти­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

8. Саша при­гла­сил Петю в гости, ска­зав, что живёт в де­ся­том подъ­ез­де в квар­ти­ре № 333, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом де­вя­ти­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

9. Тре­нер по­со­ве­то­вал Ан­дрею в пер­вый день за­ня­тий про­ве­сти на бе­го­вой до­рож­ке 15 минут, а на каж­дом сле­ду­ю­щем за­ня­тии уве­ли­чи­вать время, про­ведённое на бе­го­вой до­рож­ке, на 7 минут. За сколь­ко за­ня­тий Ан­дрей про­ведёт на бе­го­вой до­рож­ке в общей слож­но­сти 2 часа 25 минут, если будет сле­до­вать со­ве­там тре­не­ра?

10. Врач про­пи­сал па­ци­ен­ту при­ни­мать ле­кар­ство по такой схеме: в пер­вый день он дол­жен при­нять 3 капли, а в каж­дый сле­ду­ю­щий день — на 3 капли боль­ше, чем в преды­ду­щий. При­няв 30 ка­пель, он ещё 3 дня пьёт по 30 ка­пель ле­кар­ства, а потом еже­днев­но умень­ша­ет приём на 3 капли. Сколь­ко пу­зырь­ков ле­кар­ства нужно ку­пить па­ци­ен­ту на весь курс приёма, если в каж­дом со­дер­жит­ся 20 мл ле­кар­ства (что со­став­ля­ет 250 ка­пель)?

11. Врач про­пи­сал па­ци­ен­ту при­ни­мать ле­кар­ство по такой схеме: в пер­вый день он дол­жен при­нять 20 ка­пель, а в каж­дый сле­ду­ю­щий день — на 3 капли боль­ше, чем в преды­ду­щий. После 15 дней приёма па­ци­ент де­ла­ет пе­ре­рыв в 3 дня и про­дол­жа­ет при­ни­мать ле­кар­ство по об­рат­ной схеме: в 19-й день он при­ни­ма­ет столь­ко же ка­пель, сколь­ко и в 15-й день, а затем еже­днев­но умень­ша­ет дозу на 3 капли, пока до­зи­ров­ка не ста­нет мень­ше 3 ка­пель в день. Сколь­ко пу­зырь­ков ле­кар­ства нужно ку­пить па­ци­ен­ту на весь курс приёма, если в каж­дом со­дер­жит­ся 200 ка­пель?

12. Про­из­ве­де­ние де­ся­ти иду­щих под­ряд чисел раз­де­ли­ли на 7. Чему может быть равен оста­ток?

13. Сколь­ки­ми спо­со­ба­ми можно по­ста­вить в ряд два оди­на­ко­вых крас­ных ку­би­ка, три оди­на­ко­вых зелёных ку­би­ка и один синий кубик?

14. В бак объёмом 38 лит­ров каж­дый час, на­чи­ная с 12 часов, на­ли­ва­ют пол­ное ведро воды объёмом 8 лит­ров. Но в днище бака есть не­боль­шая щель, и из неё за час вы­те­ка­ет 3 литра. В какой мо­мент вре­ме­ни (в часах) бак будет за­пол­нен пол­но­стью.

15. Какое наи­мень­шее число иду­щих под­ряд чисел нужно взять, чтобы их про­из­ве­де­ние де­ли­лось на 7?

16. В ре­зуль­та­те па­вод­ка кот­ло­ван за­пол­нил­ся водой до уров­ня 2 метра. Стро­и­тель­ная помпа не­пре­рыв­но от­ка­чи­ва­ет воду, по­ни­жая её уро­вень на 20 см в час. Под­поч­вен­ные воды, на­о­бо­рот, по­вы­ша­ют уро­вень воды в кот­ло­ва­не на 5 см в час. За сколь­ко часов ра­бо­ты помпы уро­вень воды в кот­ло­ва­не опу­стит­ся до 80 см?

17. В меню ре­сто­ра­на име­ет­ся 6 видов са­ла­тов, 3 вида пер­вых блюд, 5 видов вто­рых блюд и 4 вида де­сер­та. Сколь­ко ва­ри­ан­тов обеда из са­ла­та, пер­во­го, вто­ро­го и де­сер­та могут вы­брать по­се­ти­те­ли этого ре­сто­ра­на?

18. Неф­тя­ная ком­па­ния бурит сква­жи­ну для до­бы­чи нефти, ко­то­рая за­ле­га­ет, по дан­ным гео­ло­го­раз­вед­ки, на глу­би­не 3 км. В те­че­ние ра­бо­че­го дня бу­риль­щи­ки про­хо­дят 300 мет­ров в глу­би­ну, но за ночь сква­жи­на вновь «за­или­ва­ет­ся», то есть за­пол­ня­ет­ся грун­том на 30 мет­ров. За сколь­ко ра­бо­чих дней неф­тя­ни­ки про­бу­рят сква­жи­ну до глу­би­ны за­ле­га­ния нефти?

19. Какое наи­мень­шее число иду­щих под­ряд чисел нужно взять, чтобы их про­из­ве­де­ние де­ли­лось на 9?

20. В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций:

• за 2 зо­ло­тых мо­не­ты по­лу­чить 3 се­реб­ря­ных и одну мед­ную;

• за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тых и одну мед­ную.

У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 50 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая?

21. На по­верх­но­сти гло­бу­са фло­ма­сте­ром про­ве­де­ны 12 па­рал­ле­лей и 22 ме­ри­ди­а­на. На сколь­ко ча­стей про­ведённые линии раз­де­ли­ли по­верх­ность гло­бу­са?

Ме­ри­ди­ан — это дуга окруж­но­сти, со­еди­ня­ю­щая Се­вер­ный и Южный по­лю­сы. Па­рал­лель — это окруж­ность, ле­жа­щая в плос­ко­сти, па­рал­лель­ной плос­ко­сти эк­ва­то­ра.

22. В кор­зи­не лежит 50 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 28 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 24 гри­бов хотя бы один груздь. Сколь­ко груз­дей в кор­зи­не?

23. Груп­па ту­ри­стов пре­одо­ле­ла гор­ный пе­ре­вал. Пер­вый ки­ло­метр подъёма они пре­одо­ле­ли за 50 минут, а каж­дый сле­ду­ю­щий ки­ло­метр про­хо­ди­ли на 15 минут доль­ше преды­ду­ще­го. По­след­ний ки­ло­метр перед вер­ши­ной был прой­ден за 95 минут. После де­ся­ти­ми­нут­но­го от­ды­ха на вер­ши­не ту­ри­сты на­ча­ли спуск, ко­то­рый был более по­ло­гим. Пер­вый ки­ло­метр после вер­ши­ны был прой­ден за час, а каж­дый сле­ду­ю­щий на 10 минут быст­рее преды­ду­ще­го. Сколь­ко часов груп­па за­тра­ти­ла на весь марш­рут, если по­след­ний ки­ло­метр спус­ка был прой­ден за 10 минут.

24. На коль­це­вой до­ро­ге рас­по­ло­же­ны че­ты­ре бен­зо­ко­лон­ки: A, B, C и D. Рас­сто­я­ние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все рас­сто­я­ния из­ме­ря­ют­ся вдоль коль­це­вой до­ро­ги в крат­чай­шую сто­ро­ну). Най­ди­те рас­сто­я­ние между B и C. Ответ дайте в ки­ло­мет­рах.

25. На коль­це­вой до­ро­ге рас­по­ло­же­ны че­ты­ре бен­зо­ко­лон­ки: A, B, C и D. Рас­сто­я­ние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все рас­сто­я­ния из­ме­ря­ют­ся вдоль коль­це­вой до­ро­ги в крат­чай­шую сто­ро­ну). Най­ди­те рас­сто­я­ние между B и C.

26. В клас­се учит­ся 25 уча­щих­ся. Не­сколь­ко из них хо­ди­ли в кино, 18 че­ло­век хо­ди­ли в театр, причём и в кино, и в театр хо­ди­ли 12 че­ло­век. Из­вест­но, что трое не хо­ди­ли ни в кино, ни в театр. Сколь­ко че­ло­век из клас­са хо­ди­ли в кино?

27. По эм­пи­ри­че­ско­му за­ко­ну Мура сред­нее число тран­зи­сто­ров на мик­ро­схе­мах каж­дый год удва­и­ва­ет­ся. Из­вест­но, что в 2005 году сред­нее число тран­зи­сто­ров на мик­ро­схе­ме рав­ня­лось 520 млн. Опре­де­ли­те, сколь­ко в сред­нем мил­ли­о­нов тран­зи­сто­ров было на мик­ро­схе­ме в 2003 году.

28. В пер­вом ряду ки­но­за­ла 24 места, а в каж­дом сле­ду­ю­щем на 2 боль­ше, чем в преды­ду­щем. Сколь­ко мест в вось­мом ряду?

29. На палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жёлтого и зелёного цвета. Если рас­пи­лить палку по крас­ным ли­ни­ям, то по­лу­чит­ся 5 кус­ков, если по жёлтым — 7 кус­ков, а если по зелёным — 11 кус­ков. Сколь­ко кус­ков по­лу­чит­ся, если рас­пи­лить палку по ли­ни­ям всех трёх цве­тов?

30.В ма­га­зи­не бы­то­вой тех­ни­ки объём про­даж хо­ло­диль­ни­ков носит се­зон­ный ха­рак­тер. В ян­ва­ре было про­да­но 10 хо­ло­диль­ни­ков, и в три по­сле­ду­ю­щих ме­ся­ца про­да­ва­ли по 10 хо­ло­диль­ни­ков. С мая про­да­жи уве­ли­чи­ва­лись на 15 еди­ниц по срав­не­нию с преды­ду­щим ме­ся­цем. С сен­тяб­ря объём про­даж начал умень­шать­ся на 15 хо­ло­диль­ни­ков каж­дый месяц от­но­си­тель­но преды­ду­ще­го ме­ся­ца. Сколь­ко хо­ло­диль­ни­ков про­дал ма­га­зин за год?

31. В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций:

1) за 3 зо­ло­тых мо­не­ты по­лу­чить 4 се­реб­ря­ных и одну мед­ную;

2) за 6 се­реб­ря­ных монет по­лу­чить 4 зо­ло­тых и одну мед­ную.

У Ни­ко­лы были толь­ко се­реб­ря­ные мо­не­ты. После по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 35 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лы?

32. Саша при­гла­сил Петю в гости, ска­зав, что живёт в седь­мом подъ­ез­де в квар­ти­ре № 462, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом се­ми­этаж­ный. На каком этаже живёт Саша? (На каж­дом этаже число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

33. Во всех подъ­ез­дах дома оди­на­ко­вое число эта­жей, а на каж­дом этаже оди­на­ко­вое число квар­тир. При этом число эта­жей в доме боль­ше числа квар­тир на этаже, число квар­тир на этаже боль­ше числа подъ­ез­дов, а число подъ­ез­дов боль­ше од­но­го. Сколь­ко эта­жей в доме, если всего в нём 110 квар­тир?

34. Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за пры­жок. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 6 прыж­ков, на­чи­ная пры­гать из на­ча­ла ко­ор­ди­нат?

35. В кор­зи­не лежат 40 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 17 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 25 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

36. В кор­зи­не лежат 25 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 11 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 16 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

37. В кор­зи­не лежат 30 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 12 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 20 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

38. На гло­бу­се фло­ма­сте­ром про­ве­де­ны 17 па­рал­ле­лей (вклю­чая эк­ва­тор) и 24 ме­ри­ди­а­на. На сколь­ко ча­стей про­ведённые линии раз­де­ля­ют по­верх­ность гло­бу­са?

39. Улит­ка за день за­пол­за­ет вверх по де­ре­ву на 4 м, а за ночь спол­за­ет на 3 м. Вы­со­та де­ре­ва 10 м. За сколь­ко дней улит­ка впер­вые до­ползёт до вер­ши­ны де­ре­ва?

40. Улит­ка за день за­пол­за­ет вверх по де­ре­ву на 4 м, а за ночь спол­за­ет на 1 м. Вы­со­та де­ре­ва 13 м. За сколь­ко дней улит­ка впер­вые до­ползёт до вер­ши­ны де­ре­ва?

41. Хо­зя­ин до­го­во­рил­ся с ра­бо­чи­ми, что они вы­ко­па­ют ему ко­ло­дец на сле­ду­ю­щих усло­ви­ях: за пер­вый метр он за­пла­тит им 4200 руб­лей, а за каж­дый сле­ду­ю­щий метр — на 1300 руб­лей боль­ше, чем за преды­ду­щий. Сколь­ко денег хо­зя­ин дол­жен будет за­пла­тить ра­бо­чим, если они вы­ко­па­ют ко­ло­дец глу­би­ной 11 мет­ров?

42. Хо­зя­ин до­го­во­рил­ся с ра­бо­чи­ми, что они ко­па­ют ко­ло­дец на сле­ду­ю­щих усло­ви­ях: за пер­вый метр он за­пла­тит им 3500 руб­лей, а за каж­дый сле­ду­ю­щий метр — на 1600 руб­лей боль­ше, чем за преды­ду­щий. Сколь­ко денег хо­зя­ин дол­жен будет за­пла­тить ра­бо­чим, если они вы­ко­па­ют ко­ло­дец глу­би­ной 9 мет­ров?

43. В кор­зи­не лежит 45 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 23 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 24 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

44. В кор­зи­не лежит 25 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 11 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 16 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

45. Спи­сок за­да­ний вик­то­ри­ны со­сто­ял из 25 во­про­сов. За каж­дый пра­виль­ный ответ уче­ник по­лу­чал 7 очков, за не­пра­виль­ный ответ с него спи­сы­ва­ли 10 очков, а при от­сут­ствии от­ве­та да­ва­ли 0 очков. Сколь­ко вер­ных от­ве­тов дал уче­ник, на­брав­ший 42 очка, если из­вест­но, что по край­ней мере один раз он ошиб­ся?

46. На палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жел­то­го и зе­ле­но­го цвета. Если рас­пи­лить палку по крас­ным ли­ни­ям, то по­лу­чит­ся 5 кус­ков, если по жел­тым ― 7 кус­ков, а если по зе­ле­ным ― 11 кус­ков. Сколь­ко кус­ков по­лу­чит­ся, если рас­пи­лить палку по ли­ни­ям всех трех цве­тов?

47. Улит­ка за день за­пол­за­ет вверх по де­ре­ву на 2 м, а за ночь спол­за­ет на 1 м. Вы­со­та де­ре­ва 11 м. За сколь­ко дней улит­ка до­ползёт от ос­но­ва­ния до вер­ши­ны де­ре­ва?

48. Улит­ка за день за­пол­за­ет вверх по де­ре­ву на 4 м, а за ночь спол­за­ет на 2 м. Вы­со­та де­ре­ва 14 м. За сколь­ко дней улит­ка до­ползёт от ос­но­ва­ния до вер­ши­ны де­ре­ва?

49. Пря­мо­уголь­ник раз­бит на че­ты­ре мень­ших пря­мо­уголь­ни­ка двумя пря­мо­ли­ней­ны­ми раз­ре­за­ми. Пе­ри­мет­ры трёх из них, на­чи­ная с ле­во­го верх­не­го и далее по ча­со­вой стрел­ке, равны 24, 28 и 16. Най­ди­те пе­ри­метр четвёртого пря­мо­уголь­ни­ка.

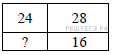
50. В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций:

1) за 2 зо­ло­тых мо­не­ты по­лу­чить 3 се­реб­ря­ных и одну мед­ную;

2) за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тых и одну мед­ную.

У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 50 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая?

 

 

51. Пря­мо­уголь­ник раз­бит на че­ты­ре мень­ших пря­мо­уголь­ни­ка двумя пря­мо­ли­ней­ны­ми раз­ре­за­ми. Пе­ри­мет­ры трёх из них, на­чи­ная с ле­во­го верх­не­го и далее по ча­со­вой стрел­ке, равны 24, 28 и 16. Най­ди­те пе­ри­метр четвёртого пря­мо­уголь­ни­ка.

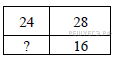
52. В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций:

1) за 4 зо­ло­тых мо­не­ты по­лу­чить 5 се­реб­ря­ных и одну мед­ную;

2) за 7 се­реб­ря­ных монет по­лу­чить 5 зо­ло­тых и одну мед­ную.

У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 90 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая?

53. Во всех подъездах дома одинаковое число этажей, а на каждом этаже — одинаковое число квартир. При этом число подъездов дома меньше числа квартир на этаже, число квартир на этаже меньше числа этажей, число подъездов больше одного, а число этажей не более 24. Сколько этажей в доме, если в нем всего 156 квартир?

54. В классе учится 26 учащихся. Несколько из них слушают рок, 14 человек слушают рэп, причем и рок, и рэп слушают всего лишь трое. Известно, что четверо не слушают ни рок, ни рэп. Сколько человек из класса слушают рок?

55. В садке лежат 35 рыб: окуни и плотвички. Известно, что среди любых 21 рыбы имеется хотя бы одна плотвичка, а среди любых 16 рыб — хотя бы один окунь. Сколько плотвичек в садке?

56. На поверхности глобуса маркером проведены 30 параллелей и 24 меридиана. На сколько частей проведенные линии разделили поверхность глобуса? (меридиан — это дуга окружности, соединяющая Северный и Южный полюсы, а параллель — это граница сечения глобуса плоскостью, параллельной плоскости экватора).

57. В доисторическом обменном пункте можно было совершить одну из двух операций:— за 2 шкуры пещерного льва получить 5 шкур тигра и 1 шкуру кабана;— за 7 шкур тигра получить 2 шкуры пещерного льва и 1 шкуру кабана.У Уна, сына Быка, были только шкуры тигра. После нескольких посещений обменного пункта шкур тигра у него не прибавилось, шкур пещерного льва не появилось, зато появилось 80 шкур кабана. На сколько, в итоге, уменьшилось количество шкур тигра у Уна, сына Быка?

58. В войсковой части 32103 имеется 3 вида салата, 2 вида первого блюда, 3 вида второго блюда и на выбор компот или чай. Сколько вариантов обеда, состоящего обязательно из одного салата, одного первого блюда, одного второго блюда и одного напитка, могут выбрать военнослужащие этой войсковой части?

59. Улитка за день заползает вверх по дереву на 5 метров, а за ночь сползает вниз на 3 метра. Высота дерева 17 метров. На какой день улитка впервые доползет до вершины дерева?

60. Сколькими способами можно поставить в ряд три одинаковых желтых кубика, один синий кубик и один зеленый кубик?

61. Произведение шестнадцати идущих подряд натуральных чисел разделили на 11. Чему может быть равен остаток от деления?

62. Каждую минуту бактерия делится на две новые бактерии. Известно, что весь объем трехлитровой банки бактерии заполняют за 4 часа. За сколько секунд бактерии заполняют четверть банки?

63. Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся?

64. Кузнечик прыгает по прямой дороге длина одного прыжка 1 см. сначала он прыгает 11 прыжков вперед потом 3 назад потом опять 11 прыжков и затем назад 3 прыжка и так далее сколько прыжков он сделает к моменту когда впервые окажется на расстоянии 100 см. от начала.

65. На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, то получится 7 кусков, если по жёлтым — 13 кусков, а если по зелёным — 5 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

66. В обменном пункте можно совершить одну из двух операций:• за 2 золотых монеты получить 3 серебряных и одну медную;• за 5 серебряных монет получить 3 золотых и одну медную.У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

67. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами.Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

68. В обменном пункте можно совершить одну из двух операций:1) за 4 золотых монеты получить 5 серебряных и одну медную; 2) за 7 серебряных монет получить 5 золотых и одну медную. У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет?

69. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 12 м. За сколько дней улитка доползёт от основания до вершины дерева?

70. Список заданий викторины состоял из 32 вопросов. За каждый правильный ответ ученик получает 5 очков. За неправильный списывали 9, при отсуттвии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 баллов, если он по крайней мере 2 раза ошибся?

71. Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?

72. Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?

73. Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 18, 12 и 20. Найдите площадь четвёртого прямоугольника.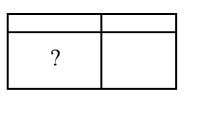

74. Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.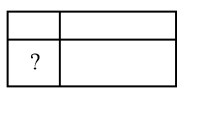

75. В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 85, во втором — 77, в третьем — 71, а сумма чисел в каждой строке больше 12, но меньше 15. Сколько всего строк в таблице?

76. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав 10 прыжков, начиная прыгать из начала координат?

77. Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)

78. В обменном пункте можно совершить одну из двух операций:• за 2 золотые монеты получить 3 серебряные и одну медную;• за 7 серебряных монет получить 3 золотые и одну медную.У Николая были только серебряные монеты. После обменного пункта золотых монет у него не появилось, зато появилось 20 медных. На сколько уменьшилось количество серебряных монет у Николая?

79. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав 11 прыжков, начиная прыгать из начала координат?

80. На кольцевой дороге расположены четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 35 км, между А и В — 20 км, между В и Г — 20 км, между Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.

81. В обменном пункте можно совершить одну из двух операций:• за 4 золотые монеты получить 5 серебряных и одну медную;• за 7 серебряных монет получить 5 золотых и одну медную.У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, Золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая.

82. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат?

83. В обменном пункте можно совершить одну из двух операций:• за 5 золотых монет получить 4 серебряные и одну медную;• за 10 серебряных монет получить 7 золотых и одну медную.У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 60 медных. На сколько уменьшилось количество серебряных монет у Николая?

84. В обменном пункте можно совершить одну из двух операций:• за 5 золотых монет получить 6 серебряных и одну медную;• за 8 серебряных монет получить 6 золотых и одну медную.У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 55 медных. На сколько уменьшилось количество серебряных монет у Николая?

85. Во всех подъездах дома одинаковое число этажей, и па всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 105 квартир?

86. В обменном пункте можно совершить одну из двух операций:1) за 3 золотых монеты получить 4 серебряных и одну медную;2) за 7 серебряных монет получить 4 золотых и одну медную.У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 42 медных. На сколько уменьшилось количество серебряных монет у Николы?

ОТВЕТЫ

infourok.ru

Наполеон из слоёного теста со сгущенкой. Торт Наполеон из готового слоеного теста со сгущенкой. На магазинных полках встречаются два вида теста: уже сформированное в листы и просто замороженное.

Сколько вариантов обеда могут выбрать посетители ресторана. Формулировка задачи: В меню ресторана имеется A видов салатов, B видов первых блюд, C видов вторых блюд и D видов десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана? Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку). Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения. В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта.

Перед подачей десерт следует украсить веточкой мяты или целыми ягодами.

Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана? Поскольку существует 6 вариантов выбора салата, 3 варианта выбора первого блюда, 5 вариантов выбора второго блюда и 4 варианта выбора десерта, число вариантов обеда можно посчитать следующим образом: 6 ⋅ 3 ⋅ 5 ⋅ 4 = 360. В общем виде решение данной задачи на смекалку выглядит следующим образом: ЧИСЛО ВАРИАНТОВ ОБЕДА = A ⋅ B ⋅ C ⋅ D. где A – число видов салата, B – число видов первых блюд, C – число видов вторых блюд, D – число видов десерта. Осталось лишь подставить все значения и получить ответ. Поделитесь статьей с одноклассниками « Сколько вариантов обеда могут выбрать посетители ресторана – как решать ». Нашли ошибку?

Способ приготовления: Овощи хорошенечко промываем в воде, даем им обсохнуть и приступаем.

Какую закуску приготовить для праздничного стола? Какой использовать для этого рецепт? Рулет из лаваша с крабовыми палочками – это идеальное изделие, которое послужит отличной закуской для любого обеденного или праздничного стола. Сегодня мы рассмотрим несколько вариантов ее приготовления. Какой из них взять себе на заметку – решать исключительно вам.

Выделите текст и нажмите Ctrl + Enter. В воинской части 32103 имеется 3 вида салата,2 вида первых блюда,3 вида второго блюда и на выбор компот или чай.Сколько вариантов обеда,состоящего обязательно из одного салата,одного первого блюда,одного второго блюда и одного напитка,могут выбрать военнослужащие этой воинской части? Ответ оставил Гость. Если подробно, то 3 вида салата и 2 вида первых блюд дают 3х2=6 вариантов.

Если вы в поиске чем наполнить тарталетки для праздничного стола – смело рекомендую … Cалат с черносливом и курицей «Именинник» В поисках новых салатов нашла очень интересный рецепт салата с черносливом и курицей.

Эти 6 вариантов в сочетании с каждым из 3-х видов 2-го блюда дают 6х3=18 вариантов, которые в сочетании с компотом или чаем дают 18х2=36 вариантов. А коротко: 3х2х3х2=36. Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Математика.

В меню ре­сто­ра­на имеется 6 видов салатов, 3 вида пер­вых блюд, 5 видов вто­рых блюд и 4 вида десерта.

Жаль, что рецепт с фото не может передать аппетитный аромат этого блюда.

Сколь­ко вариантов обеда из салата, первого, вто­ро­го и де­сер­та могут вы­брать посетители этого ресторана? Салат можно выбрать шестью способами, первое — тремя, второе — пятью, десерт — четырьмя. Следовательно, всего 6 · 3 · 5 · 4 = 360 вариантов обеда.

1 крупный болгарский перец; 3-4 спелых помидора; банка тунца в собственном соку; оливковое масло 3-4 ст.

limo-exclusive.ru

В войсковой части 32103 имеется 3 вида салата 2 вида первого блюда

Сколько вариантов обеда могут выбрать посетители ресторана. Формулировка задачи: В меню ресторана имеется A видов салатов, B видов первых блюд, C видов вторых блюд и D видов десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана? Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку). Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения. В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта.

Тесто замешивается обычной вилкой без помощи рук. Чебуреки получаются сказочно вкусными, хрустящими, пузырчатыми и сочными внутри!    Рецепт № 1 Для вкусных, сочных чебуреков с хрустящей пузырчатой корочкой, главное — хоро… Очень вкусный и простой рецепт бисквитного торта в домашних условиях. Бисквитный торт принято считать самым популярным в разделе выпечки. Стоит отметить, что кулинарным шедевром он точно не будет,

Майонез у меня густой, он образует симпатичные волны по краю салата.

Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана? Поскольку существует 6 вариантов выбора салата, 3 варианта выбора первого блюда, 5 вариантов выбора второго блюда и 4 варианта выбора десерта, число вариантов обеда можно посчитать следующим образом: 6 ⋅ 3 ⋅ 5 ⋅ 4 = 360. В общем виде решение данной задачи на смекалку выглядит следующим образом: ЧИСЛО ВАРИАНТОВ ОБЕДА = A ⋅ B ⋅ C ⋅ D. где A – число видов салата, B – число видов первых блюд, C – число видов вторых блюд, D – число видов десерта. Осталось лишь подставить все значения и получить ответ. Поделитесь статьей с одноклассниками « Сколько вариантов обеда могут выбрать посетители ресторана – как решать ». Нашли ошибку?

Сюда же выложите отварной рис, перемешайте и прогрейте на небольшом огне некоторое время.

Салат с креветками и кальмарами подойдет как для званого ужина или трапезы в кругу семьи, так и для праздничного стола. Продукты сочетаются идеально! Для оформления праздничного стола, для создания оригинальных композиций и в качестве сувенира на Пасху может быть использована подставка для пасхальных яиц, куда можно

Выделите текст и нажмите Ctrl + Enter. В воинской части 32103 имеется 3 вида салата,2 вида первых блюда,3 вида второго блюда и на выбор компот или чай. Сколько вариантов обеда, состоящего обязательно из одного салата, одного первого блюда, одного второго блюда и одного напитка, могут выбрать военнослужащие этой воинской части? Ответ оставил Гость. Если подробно, то 3 вида салата и 2 вида первых блюд дают 3х2=6 вариантов.

Перед подачей украшаем салат натертыми на мелкой терке желтками, по кругу вставляем чипсы и украшаем сверху порезанными на 4 части маслинами.

Эти 6 вариантов в сочетании с каждым из 3-х видов 2-го блюда дают 6х3=18 вариантов, которые в сочетании с компотом или чаем дают 18х2=36 вариантов. А коротко: 3х2х3х2=36. Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Математика.

В меню ре­сто­ра­на имеется 6 видов салатов, 3 вида пер­вых блюд, 5 видов вто­рых блюд и 4 вида десерта.

Скатываю получившееся в форму шара, который на 60 минут оставляю в теплом не продуваемом месте.

Сколь­ко вариантов обеда из салата, первого, вто­ро­го и де­сер­та могут вы­брать посетители этого ресторана? Салат можно выбрать шестью способами, первое — тремя, второе — пятью, десерт — четырьмя. Следовательно, всего 6 · 3 · 5 · 4 = 360 вариантов обеда.

Первый слой, потихоньку утрамбовывая, укладываем из белой массы.

videofanat.ru

---

Смотрите также

• 
  В войсковой части 32103 имеется 3 вида салата 2 вида первого блюда
• 
  Не хватай блюдо первым и не дуй в жидкое чтобы везде брызгало
• 
  Не хватай блюдо первым и не дуй в жидкое чтобы везде брызгало
• 
  Что можно есть кормящей маме в первый месяц после родов список блюд
• 
  Что можно есть кормящей маме в первый месяц после родов список блюд
• 
  Какие блюда можно кушать кормящей маме в первый месяц после родов
• 
  Капуста входит в рецептуру первых блюд харчо уха борщ щи рассольник
• 
  Какие блюда можно кушать кормящей маме в первый месяц после родов
• 
  Капуста входит в рецептуру первых блюд харчо уха борщ щи рассольник
• 
  Рецепты с фото первых блюд простые и вкусные и недорогие популярные
• 
  Рецепты с фото первых блюд простые и вкусные и недорогие популярные