Содержание
Расчет штата поваров и суточного наряда — Мегаобучалка
Штатная численность работников столовой определяется исходя из их количества, необходимого для приготовления обеденных блюд.
Расчет ведется в условных блюдах, при этом учитывают нормы времени, установленные для приготовления единицы изделия.
Расчет количества поваров ведут по формуле:
, чел (13)
где: Ny– количество условных блюд;
ty – норма времени на одно условное блюдо (0,028 ч)
t – продолжительность приготовления блюд, которая зависит от условий работы столовой воинской части , ч.
1,15 – коэффициент, учитывающий рост производительности труда
Таблица 4. Расчет количества условных блюд
Исходя из этого для приготовления обеда необходимо:
Таким образом, потребность в поварах для максимальной смены составит 16 чел.
Часть поваров этой смены готовит также ужин. Другая смена поваров должна готовить завтрак, состоящий из одного горячего блюда и чая. В состав этой смены берется 20 % от числа поваров, занятых приготовлением обеда.
В нашем случае это составит 4 чел.
Третья смена поваров отдыхает, с поварами могут проводиться занятия по боевой, политической и специальной подготовке. В ее состав входит до 40% числа поваров, приготовляющих обед. Это составит 7 человек. Таким образом, общее количество поваров составит 27 человек.
Состав смен окончательно определяют при составлении графика работы поваров. График составляют на 7 дней с указанием времени работы каждой смены и с учетом выходных дней.
Однако в воинской части количество поваров в столовой устанавливается ее штатом.
В соответствии с Руководством по организации питания личного состава воинских частей и учреждений Вооруженных Сил Российской Федерации, при определении количества поваров исходят из следующих норм:
в столовой, где питаются:
· до 150 человек — 3 повара,
· от 151 до 200 человек — 4 повара,
· в последующем на каждые 125 питающихся добавляется 1 повар.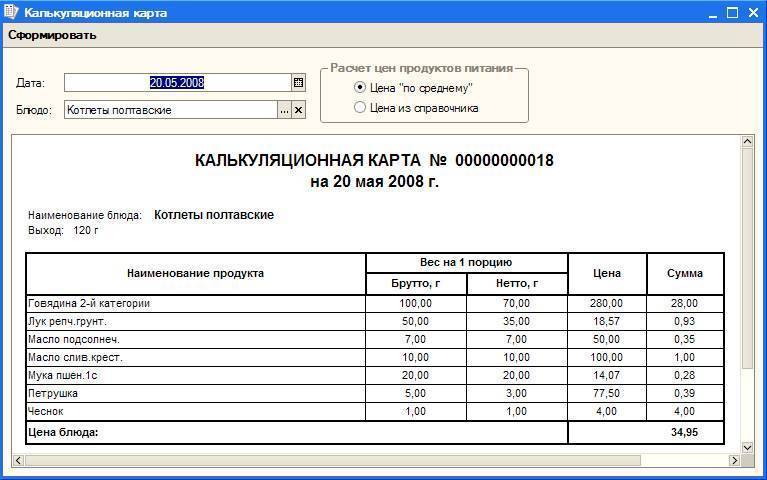
Инструктор-повар содержится при численности питающихся свыше 500 человек и в расчетное количество поваров не засчитывается, а мастер по технологии приготовления пищи — при численности питающихся свыше 1000 человек.
Составим график работы поваров.
График работы поваров
Повара
| Дни, недели и время
| Количество дежурств
| Количество часов
| |||||||||||||
1
| 2
| 3
| 4
| 5
| 6
| 7
| ||||||||||
Смена
| ||||||||||||||||
| 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |||
20.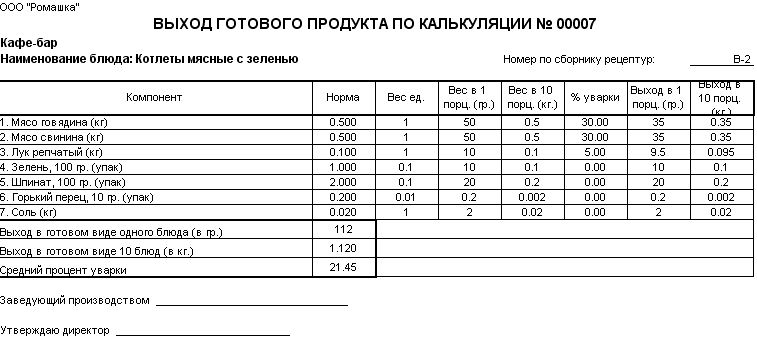 00-8.00 00-8.00
| 8.00-20.00 | 20.00-8.00 | 8.00-20.00 | 20.00-8.00 | 8.00-20.00 | 20.00-8.00 | 8.00-20.00 | 20.00-8.00 | 8.00-20.00 | 20.00-8.00 | 8.00-20.00 | 20.00-8.00 | 8.00-20.00 | |||
График работы поваров, подписанный инструктором-поваром утверждается начальником столовой.
Расчет количества лиц суточного наряда столовой для цехов и помещений производят на основании норм выработки полуфабрикатов, количества натуральных или условных единиц продукции, которые повар или смена должны выработать в единицу времени.
В соответствии с Руководством по организации питания личного состава воинских частей и учреждений Вооруженных Сил Российской Федерации, суточный наряд по столовой назначается для уборки помещений, доставки продовольствия со склада в столовую, очистки и дочистки свежих картофеля и овощей, сервировки обеденных столов, мытья столовой и кухонной посуды и других подсобных работ.
Суточный наряд по столовой выделяется из расчета: до 100 человек питающихся в столовой — 3-4 человека, дополнительно выделяется по 2 человека на каждые последующие 100 человек питающихся.
Исходя из этого, общее количество лиц суточного наряда по столовой составит в нашем случае:
Для нарезки хлеба, порционирования сахара и их выдачи выделяется хлеборез на срок, определяемый командиром части, из расчета питающихся в данной столовой: до 500 чел. –1; 501-1000 чел. – 2 и свыше 1000 чел. – 3.
–1; 501-1000 чел. – 2 и свыше 1000 чел. – 3.
Принимаем –3 чел.
Сводная таблица
| Наименование должностей | Количество человек |
| Повар
Суточный наряд Хлеборез | 27
32 3 |
Расчет основных технико-экономических показателей работы предприятия общественного питания
333326.03.2013
Введение
Переход нашей экономики от планово
— централизованной к рыночной оказался
очень сложным. Этот этап сопровождается
падением производства, информацией, снижением
жизненного уровня населения и
нарастанием социальной напряженности
в обществе. Таких существенных негативных
последствий никто не предполагал; прогнозировалось
экономическое ухудшение в стране, но
не в таких масштабах. Почему же произошла
такая ситуация?
Можно назвать множество объективных
и субъективных причин, но ни одна из них
до конца не раскроет суть происходящего,
настолько это многоплановое и не ординарное
явление для нашей страны. Управленческий
Управленческий
персонал не был подготовлен к выполнению
своих функций в условиях рыночных отношений.
Все это сыграло негативную роль
при осуществлении
реформы в России. Отсюда можно
сделать вывод, что подготовка экономистов
новой формации, глубоко понимающих
теорию рыночной экономики и умеющих
эффективно использовать полученные знания
на практике как на макро — , так и на
микроуровне, имеет исключительно важное
значение для России.
Известно, что экономика подразделяется
на две основные области: макроэкономику
и микроэкономику.
Макроэкономика изучает
состояние, «здоровье» страны в целом.
В макроэкономике все величины рассматриваются
в агрегированном, совокупном виде: национальный
доход, валовой национальный продукт,
совокупный спрос, совокупное предложение
и д.р.
Микроэкономика связана с
отдельных экономических субъек
Она изучает деятельность предприятий,
фирм и отрасли народного хозяйства.
Именно на предприятии создается
продукция и услуги, необходимые
для производственных целей и
нужд населения. Поэтому от того как
они используют свои ресурсы, какую
выпускают продукцию по уровню качества
и конкурентоспособности, зависит экономическое
могущество страны и уровень жизни ее
граждан.
Питание является формой потребления.
По мере развития общества питание
все больше начинает носить общественно
организованный характер, т.е. развивается
общественное питание. Можно выделить
две формы организации питания:
- Индивидуально организационное питание;
- Общественное питание.
Система общественного питания
при едином назначении функционирует
в различных социально-
формах. Следует отметить различные
понятия «сфера общественного питания»
и «отрасль общественного питания».
Сфера общественного питания включает
все организационные формы
питания задачами, которых являются
восстановление и поддержание на
должном уровне здоровья людей.
Общественное питание можно рассмотреть
как отрасль, главной целью которой является
предоставление услуг населению в форме
общественно организационного питания
в обмен на его денежные доходы. Для отрасли
общественного питания характерна общность
материально-технической базы, технологической
и организационно- экономической структур.
По оценкам специалистов, в домашних условиях
готовится примерно 83% пищи, на предприятиях
общественного питания — около 17%.
Социально — экономическое значение
общественного питания выражается в условии
для роста производительности и улучшения
организации труда благодаря предоставлению
полноценного горячего питания по месту
работы и учебы населения; в обеспечении
экономии общественного труда и средств;
в создании предпосылок для увеличения
свободного времени членов общества, особенно
женщин.
Так, на промышленных
предприятиях с хорошо
сетью столовых
труда, по оценкам социологов,
на 7-8 % выше, чем там, где их
нет. Для сохранения здоровья
Для сохранения здоровья
работающих особое значение имеет организация
диетического питания. Оно способствует
увеличению отработанного времени
в расчете на одного работника, сокращению
потерь времени по болезни.
Затраты труда на
приготовление пищи в домашних
условиях примерно в 5-6 раз выше,
чем в общественном питании. Обследования
свидетельствуют, что в семье из 4 человек
на приготовление пищи тратится 4 часа
ежедневно.
Материальные затраты
в общественном питании ниже
чем, домашнем питании. В
питании. В среднем на приготовление
одного обеда в столовых требуется примерно
300 г топлива условном выражении, а дома
— в три раза больше.
Работа в домашнем
хозяйстве составляет у женщин
примерно 20,8%, у мужчин – 6,9% внерабочего
времени. Бюджет времени на
ведение домашнего хозяйства у женщин
(116 часов) примерно равен бюджету свободного
времени (120 часов). Между тем увеличение
свободного времени является важной социальной
задачей любого общества и одним из показателей
качества жизни.
Рецептуры блюд
Салат из свежих помидоров | |
Наименование сырья | Вес сырья по массе |
Помидоры свежие Зеленый лук Лук репчатый Сметана Выход | 71,8 25 23,8 20 100 |
Суп-харчо | |
Чеснок Хмели Сунели Шафран Корица Гвоздика Лук репчатый Масло сливочное Мука кукурузная Перец красный Петрушка Орехи грецкие Выход | 7,7 1,5 0,15 0,6 0,6 107 30 30 0,6 24 133 300 |
Фрикадельки в соусе | |
Говядина Хлеб пшеничный Молоко Лук репчатый Жир топленый Мука Соус томатный Выход | 103 16 24 29 11 8 75 250 |
1. Расчет основных технико-
Расчет основных технико-
показателей работы предприятия общественного
питания
1.1 Расчет производственной
Основной частью плана товарооборота
предприятия общественного
является реализация продукции собственного
производства, разрабатываемая на основе
производственной программы.
Производственная программа –
это плановое задание по выпуску
всех видов продукции собственного
производства на определенный период
с указанием вида продукции, ассортимент
и цены изделий.
На производственную программу
влияют:
— численность и состав потребителей;
— спрос на продукцию;
— мощность предприятия;
— наличие сырья и
— наличие квалифицированных
При планировании выпуска блюд необходимо
учитывать пропускную способность
зала (предприятия).
Пропускная способность зала
– характеризуется максимальным количеством
потребителей, обслуживаемых за период
времени (смену, месяц).
ПС=(ВР×Чм)/ВП
(1)
где ВР – время работы
зала за день, мин.
Чм – число мест;
ВП – время приема пищи одним
посетителем, мин.
или
ПС=(ВР×S)/(ВП×Пн), где
(2)
S – площадь обеденного зала,
м2;
Пн – норма площади на одного
посетителя (1,9м2).
k – коэффициент заполнения
зала с учетом интенсивности потока посетителей.
Другим показателем, характеризующим
интенсивность потока потребителей
и пропускную способность предприятия,
является оборачиваемость одного
места. Это – число потребителей, приходящееся
на одно место на предприятии за день.
Ом=Чплан/Чм
(3)
где Чм – число мест;
Чплан – плановое число мест.
Для обновления плана выпуска блюд
используют различные методы планирования
выпуска блюд:
- на основе планового меню;
- по данным изучения спроса потребителей;
- по численности потребителей;
- по данным ожидаемого выполнения плана и расчета сопоставимой базы выпуска блюд;
- на основе расчета производственной мощности кухни и пропускной способности зала.
Плановое меню представляет собой
перечень блюд по ассортименту и количеству,
подлежащих изготовлению в течение
определенного периода. На основе планового
меню определяется среднесуточный выпуск
блюд в ассортименте, с указанием массы
порций и их цены.
Разработка планового меню основывается
на большом информационном материале,
отражающем данные о численности
и составе потребителей, колебания
спроса на кулинарную продукцию, перспективы
снабжения предприятий сырьем и продуктами.
Сущность метода расчета
выпуска блюд по данным изучения спроса
заключается в наблюдении за ежедневной
реализацией блюд в течение месяца.
На предприятиях с относительно
постоянным контенгентом потребителей
(столовая при школах, училищах, промышленных
предприятиях) расчет плана выпуска блюд
осуществляется на основе данных о численности
потребителей. При этом учитывается процент
охвата потребителей общественным питанием,
количество дней работы ПОП, среднее число
блюд на одного потребителя и стоимость
дневного рациона.
Годовой (квартальный, месячный)
план выпуска блюд можно рассчитать
по формуле:
ВБплан=ПСмакс×Кпс×Б×Д
(4)
где ВБплан – плановый
выпуск блюд за период;
ПСмакс – пропускная способность
обеденного зала, чел.
Кпс – коэффициент использования
пропускной способности обеденного
зала;
Б – среднее количество блюд на
одного посетителя;
Д – количество рабочих дней
в плановом периоде.
Одним из методов определения плана
выпуска первых блюд является расчет
производственной мощности кухни столовой.
Производственная мощность – максимально
возможный выпуск продукции предприятием
(цехом) в единицу времени (смену,
сутки, месяц, год). При расчете мощности
учитывают применение новой техники и
технологии; рациональных методов организации
труда. Рассчитывается в натуральных или
условных показателях: блюдах, условных
блюдах. Расчет производственной мощности
производится по основным выдам продукции
с учетом мощности ведущего экономического
оборудования (котлов, плит, жарочных установок).
М=((В–П)×Ок×Кз)/(в×Об)
(5)
где В – время работы
столовой, мин;
П – время простоя оборудования,
мин;
Ок – емкость котлов, л;
Кз – коэффициент заполнения
емкостей;
в – продолжительность одного производственного
цикла;
Об – емкость одного блюда.
Производственная мощность – величина
не постоянная. Большое внимание на
нее оказывают технический прогресс
и совершенствование организации труда
и производства, ритмичность снабжения
предприятия сырьем и др.
Данный раздел представлен таблицей
1.
Таблица 1 – Расчет производственной
программы в натуральном
Наименование блюд | Структура планируемой | Планируемое количество |
1.Салат из свежих помидоров | 25 | 127500 |
2.Суп-харчо | 30 | 153000 |
3.Фрикадельки в соусе | 45 | 229500 |
Итого: | 100 | 510000 |
1.2 Расчет потребности и
сырья
Для работы предприятий общественного
питания необходимо снабжение их сырьём,
полуфабрикатами, покупными товарами
в определенном количестве и ассортименте.
Разрабатывают план снабжения
План снабжения
в форме продуктового баланса
и состоит из 3-х разделов:
1. Определение потребности в сырье
Определение потребности в сырье
и товарах в соответствии с объемом выпуска
продукции, а так же планом оборота по
покупным товарам;
- Расчет размера запасов сырья и товаров на начало и конец планового периода;
- Планирование поступления сырья и товаров.
При планировании снабжения наиболее
сложным является определение потребности
в сырье и товарах. Возможно применение
следующих методов расчета потребности
в сырье и покупных товарах:
1. На основе индивидуальных норм
расхода сырья на единицу продукции и
плана выпуска продукции в ассортименте;
2. На основе среднегрупповых норм
расхода сырья на одно блюдо или на единицу
продукции и плана выпуска продукции в
ассортименте;
3. На основе корректировки расхода
сырья за отчетный год.
Нормы расхода отдельных видов
сырья на одно блюдо или единицу
кулинарного изделия приведены в сборниках
рецептур блюд для предприятий общественного
питания, которые указаны по массе брутто
и массе нетто, так же в приводятся нормы
выхода готовых блюд.
Для определения потребности в
сырье на отдельные виды кулинарной
продукции по индивидуальным нормам применяется
формула:
Qп = (n*q)/1000,
(6)
где: Qп — количество сырья,
необходимое для выполнения производственной
программы, кг;
n – индивидуальная норма
сырья на единицу изделия, г;
q –
количество блюд в плановом
периоде.
Среднегрупповые нормы расхода
сырья по группам блюд представляют
собой расчетную норму среднего
количества продуктов каждого наименования
на единицу массы или на одно блюд.
Среднегрупповая норма (Н) определяется
с учетом планового ассортимента выпускаемых
блюд и индивидуальных норм расхода сырья
по формуле:
Н = ∑ Нi ∙ Кi
/∑ Кi, где:
(7)
Нi—
индивидуальная норма расхода сырья на
каждое наименование блюд
Кi— количество блюд данного
наименования
∑ Кi – общее
количество блюд
После определения
общей потребности в сырье
и товарах разрабатываются
нормативы товарных запасов. Их делят
Их делят
на запасы текущего хранения и запасы
сезонного накопления.
Кондиционирование | Независимость | CDF
← предыдущий
следующий →
5.1.3 Обусловленность и независимость
Мы обсуждали условную вероятность раньше, и вы уже видели некоторые проблемы, связанные со случайными величинами и условной вероятностью. Здесь мы обсудим кондиционирование для случайных величин более подробно и представим условную PMF, условную CDF и условное ожидание. Мы хотели бы подчеркнуть, что существует только одна основная формула относительно условной вероятности, которая
\begin{выравнивание}\label{}
\nonumber P(A|B)=\frac{P(A \cap B)}{P(B)}, \textrm{ когда } P(B)>0.
\end{выравнивание}
Любая другая формула, касающаяся условной вероятности, может быть получена из приведенной выше формулы. В частности, если у вас есть две случайные величины $X$ и $Y$, вы можете написать
\begin{выравнивание}\label{}
\nonumber P(X \in C|Y \in D)=\frac{P(X \in C, Y \in D)}{P(Y \in D)}, \textrm{ где } C, D \ подмножество \mathbb{R}.
\end{выравнивание}
Условный PMF и CDF:
Помните, что PMF по определению является вероятностной мерой, то есть это $P(X=x_k)$. Таким образом, можно говорить об условном ПМФ . В частности, условная PMF $X$ для данного события $A$ определяется как
\begin{выравнивание}%\метка{}
\номер P_{X|A}(x_i)&=P(X=x_i|A) \\
\nonumber &=\frac{P(X=x_i \textrm{ и } A)}{P(A)}.
\end{выравнивание}
Пример
Я бросаю верный кубик. Пусть $X$ будет наблюдаемым числом. Найдите условную PMF для $X$, зная, что наблюдаемое число меньше $5$.
- Решение
- Здесь мы обуславливаем событие $A=\{X
. Для дискретной случайной величины $X$ и события $A$ условная PMF для $X$ при заданном $A$ определяется как
\begin{выравнивание}%\метка{}
\номер P_{X|A}(x_i)&=P(X=x_i|A) \\
\nonumber &=\frac{P(X=x_i \textrm{ и } A)}{P(A)}, \hspace{10pt} \textrm{для любого $x_i \in R_X$}.
\end{выравнивание}
Точно так же мы определяем условных CDF $X$ при заданном $A$ как
\begin{выравнивание}%\метка{}
\nonumber F_{X|A}(x)&=P(X \leq x|A).
\end{выравнивание}
Условная PMF $X$ При заданном $Y$:
В некоторых задачах мы наблюдали значение случайной величины $Y$, и нам нужно обновить PMF другой случайной величины $X$, значение которой еще не наблюдалось. В этих задачах мы используем условных PMF $X$ при заданном $Y$. Условная PMF $X$ при заданном $Y$ определяется как
\begin{выравнивание}%\метка{}
\номер P_{X|Y}(x_i|y_j)&=P(X=x_i|Y=y_j) \\
\nonumber &=\frac{P(X=x_i,Y=y_j)}{P(Y=y_j)}\\
\nonumber &=\frac{P_{XY}(x_i,y_j)}{P_Y(y_j)}.
\end{выравнивание}
Точно так же мы можем определить условную вероятность $Y$ при $X$:
\begin{выравнивание}%\метка{}
\номер P_{Y|X}(y_j|x_i)&=P(Y=y_j|X=x_i) \\
\nonumber &=\frac{P_{XY}(x_i,y_j)}{P_X(x_i)}.
\end{выравнивание}
Для дискретных случайных величин $X$ и $Y$ условных PMF $X$ при заданном $Y$ и наоборот определяются как
\begin{выравнивание}%\метка{}
\nonumber P_{X|Y}(x_i|y_j)&=\frac{P_{XY}(x_i,y_j)}{P_Y(y_j)},\\
\nonumber P_{Y|X}(y_j|x_i)&=\frac{P_{XY}(x_i,y_j)}{P_X(x_i)}
\end{выравнивание}
для любых $x_i \in R_X$ и $y_j \in R_Y$.
Независимые случайные величины:
Ранее мы определили независимые случайные величины. Теперь, когда мы увидели совместные PMF и CDF, мы можем переформулировать определение независимости.
Две дискретные случайные величины $X$ и $Y$ независимы, если
\begin{выравнивание}%\метка{}
\nonumber P_{XY}(x,y)=P_X(x) P_Y(y), \hspace{10pt} \textrm{ для всех }x,y.
\end{выравнивание}
Эквивалентно, $X$ и $Y$ независимы, если
\begin{выравнивание}%\метка{}
\nonumber F_{XY}(x,y)=F_X(x) F_Y(y), \hspace{10pt} \textrm{ для всех }x,y.
\end{align}
Рисунок 5.4: Пример сетки 5.4
Итак, если $X$ и $Y$ независимы, мы имеем
\begin{выравнивание}%\метка{}
\номер P_{X|Y}(x_i|y_j)&=P(X=x_i|Y=y_j)\\
\nonumber &=\frac{P_{XY}(x_i,y_j)}{P_Y(y_j)}\\
\nonumber &=\frac{P_X(x_i) P_Y(y_j)}{P_Y(y_j)}\\
\номер &=P_X(x_i).
\end{выравнивание}
Как и следовало ожидать, для независимых случайных величин условная PMF равна предельной PMF. Другими словами, знание значения $Y$ не дает никакой информации о $X$.
Другими словами, знание значения $Y$ не дает никакой информации о $X$.
Пример
Рассмотрим набор точек сетки, показанной на рис. 5.4. Это точки множества $G$, определенные как
\begin{выравнивание}%\метка{}
\nonumber G=\{(x,y) | х, у \in \mathbb{Z}, |х|+|у|\leq 2\}.
\end{выравнивание}
Предположим, что мы совершенно случайно выбираем точку $(X,Y)$ из этой сетки. Таким образом, каждая точка имеет вероятность $\frac{1}{13}$ быть выбранной.
- Найдите совместную и маргинальную ВМП $X$ и $Y$.
- Найдите условную PMF для $X$ при $Y=1$.
- $X$ и $Y$ независимы?
- Раствор
- Здесь обратите внимание, что
\begin{выравнивание}%\метка{}
\nonumber R_{XY}=G=\{(x,y) | х, у \in \mathbb{Z}, |х|+|у|\leq 2\}.
\end{выравнивание}
Таким образом, совместная PMF определяется выражением
\begin{уравнение}
\номер P_{XY}(x,y) = \left\{
\begin{массив}{л л}
\frac{1}{13} & \quad (x,y) \in G \\
0 & \quad \text{иначе}
\end{массив} \right.
\end{уравнение}
Чтобы найти предельную PMF $X$, $P_X(i)$, мы используем уравнение 5.1. Таким образом,
\begin{выравнивание}%\метка{}
\номер &P_X(-2)=P_{XY}(-2,0)=\frac{1}{13},\\
\nonumber &P_X(-1)=P_{XY}(-1,-1)+P_{XY}(-1,0)+P_{XY}(-1,1)=\frac{3}{13} ,\\
\номер &P_X(0)=P_{XY}(0,-2)+P_{XY}(0,-1)+P_{XY}(0,0)\\
\nonumber & \hspace{40pt} +P_{XY}(0,1)+P_{XY}(0,2)=\frac{5}{13},\\
\nonumber &P_X(1)=P_{XY}(1,-1)+P_{XY}(1,0)+P_{XY}(1,-1)=\frac{3}{13},\\
\nonumber &P_X(2)=P_{XY}(2,0)=\frac{1}{13}.
\end{выравнивание}
Точно так же мы можем найти
\begin{уравнение}
\номер P_Y(j) = \влево\{
\begin{массив}{л л}
\frac{1}{13} & \quad \text{для} j=2,-2\\
\frac{3}{13} & \quad \text{для } j=-1,1\\
\frac{5}{13} & \quad \text{для} j=0\\
0 & \quad \text{иначе}
\end{массив} \right.
\end{уравнение}
Мы можем записать это в более компактной форме как
\begin{выравнивание}%\метка{}
\nonumber P_{X}(k)=P_{Y}(k)=\frac{5-2|k|}{13}, \hspace{10pt} \textrm{ для }k=-2,-1, 0,1,2.
\end{выравнивание} - Для $i=-1,0,1$ можно написать
\begin{выравнивание}%\метка{}
\nonumber P_{X|Y}(i|1)&=\frac{P_{XY}(i,1)}{P_Y(1)}\\
\nonumber &=\frac{\frac{1}{13}}{\frac{3}{13}}=\frac{1}{3}, \hspace{10pt} \textrm{ для}i=-1 ,0,1.
\end{выравнивание}
Таким образом, мы заключаем
\begin{уравнение}
\номер P_{X|Y}(i|1) = \left\{
\begin{массив}{л л}
\frac{1}{3} & \quad \textrm{ для }i=-1,0,1 \\
0 & \quad \text{иначе}
\end{массив} \right.
\end{уравнение}
Глядя на приведенную выше условную PMF, мы заключаем, что при $Y=1$ $X$ равномерно распределено по множеству $\{-1,0,1\}$. - $X$ и $Y$ независимы от , а не от . Мы можем видеть это, поскольку условная PMF $X$ при $Y=1$ (вычисленная выше) не совпадает с предельной PMF $X$, $P_{X}(x)$.
- Здесь обратите внимание, что
Условное ожидание:
Зная, что событие $A$ произошло, мы можем вычислить условное математическое ожидание случайной величины $X$, $E[X|A]$.
Условное ожидание похоже на обычное ожидание. Разница лишь в том, что мы заменяем PMF на условный PMF. В частности, у нас есть
\begin{выравнивание}%\метка{}
\nonumber E[X|A]=\sum_{x_i \in R_{X}} x_i P_{X|A}(x_i).
\end{выравнивание}
Точно так же, учитывая, что мы наблюдали значение случайной величины $Y$, мы можем вычислить условное математическое ожидание $X$. В частности, условное ожидание $
В частности, условное ожидание $
X$ при условии, что $Y=y$ равно
\begin{выравнивание}%\метка{}
\nonumber E[X|Y=y]=\sum_{x_i \in R_{X}} x_i P_{X|Y}(x_i|y).
\end{выравнивание}
Условное ожидание $X$:
\begin{выравнивание}%\метка{}
\nonumber &E[X|A]=\sum_{x_i \in R_{X}} x_i P_{X|A}(x_i),\\
\nonumber &E[X|Y=y_j]=\sum_{x_i \in R_{X}} x_i P_{X|Y}(x_i|y_j)
\end{выравнивание}
Пример
Пусть $X$ и $Y$ такие же, как в примере 5.4.
- Найти $E[X|Y=1|$.
- Найти $E[X| -1
- Найти $E[|X| | -1
- Найти $E[|X| | -1
- Раствор
- Чтобы найти $E[X|Y=1]$, мы имеем
\begin{выравнивание}%\метка{}
\nonumber E[X|Y=1]=\sum_{x_i \in R_{X}} x_i P_{X|Y}(x_i|1).
\end{выравнивание}
В примере 5.4 мы обнаружили, что при $Y=1$ $X$ равномерно распределено по множеству $\{-1,0,1\}$. Таким образом, мы заключаем, что
\begin{выравнивание}%\метка{}
\номер E[X|Y=1]=\frac{1}{3}(-1+0+1)=0.
\end{выравнивание} - Чтобы найти $E[X| -1
\end{выравнивание}
Таким образом, у нас есть
\begin{выравнивание}%\метка{}
\nonumber E[X|A]&=\sum_{x_i \in R_{X}} x_i P_{X|A}(x_i)\\
\nonumber &=(-2)\frac{1}{8}+(-1)\frac{1}{4}+(0)\frac{1}{4}+(1)\frac{1} {4}+(2)\фракция{1}{8}=0.
\end{выравнивание} - Чтобы найти $E[|X| | -1
- Чтобы найти $E[X|Y=1]$, мы имеем
У условного ожидания есть несколько интересных свойств, которые обычно используются на практике. Таким образом, мы вернемся к условному ожиданию в разделе 5.1.5, где обсудим свойства условного ожидания, условной дисперсии и их применения.
Закон полной вероятности:
Вспомните закон полной вероятности: если $B_1, B_2, B_3,. ..$ является разбиением выборочного пространства $S$, то для любого события $A$ имеем
..$ является разбиением выборочного пространства $S$, то для любого события $A$ имеем
\begin{выравнивание}\label{}
\nonumber P(A)=\sum_{i} P(A \cap B_i)=\sum_{i} P(A | B_i) P(B_i).
\end{выравнивание}
Если $Y$ — дискретная случайная величина с диапазоном $R_Y=\{y_1,y_2,…\}$, то события $\{Y=y_1\}$, $\{Y=y_2\}$, $\{Y=y_3\}$, $\cdots$ образуют раздел демонстрационного пространства.
Таким образом, мы можем использовать закон полной вероятности. На самом деле мы уже использовали закон полной вероятности, чтобы найти предельные PMF:
\начать{выравнивать}
\nonumber P_X(x)=\sum_{y_j \in R_Y} P_{XY}(x,y_j)=\sum_{y_j \in R_Y} P_{X|Y}(x|y_j)P_Y(y_j).
\end{выравнивание}
Мы можем записать это в более общем виде как
\начать{выравнивать}
\nonumber P(X \in A)=\sum_{y_j \in R_Y} P(X \in A|Y=y_j)P_Y(y_j), \hspace{10pt} \textrm{для любого множества $A$}.
\end{выравнивание}
Аналогичную формулу можно написать и для ожидания. Действительно, если $B_1, B_2, B_3,…$ — разбиение выборочного пространства $S$, то
\begin{выравнивание}\label{}
\nonumber EX=\sum_{i} E[X|B_i]P(B_i).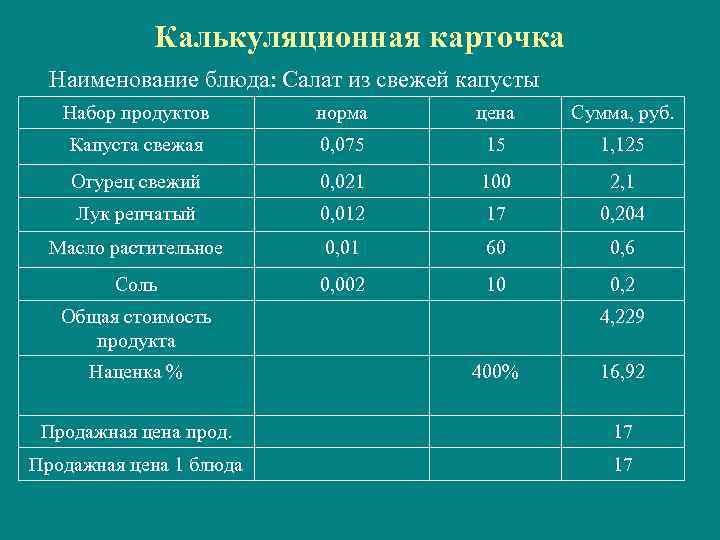
\end{выравнивание}
Чтобы убедиться в этом, просто напишите определение $E[X|B_i]$ и примените закон полной вероятности. Приведенное выше уравнение иногда называют законом полного ожидания [2].
Закон полной вероятности:
\начать{выравнивать}
\nonumber &P(X \in A)=\sum_{y_j \in R_Y} P(X \in A|Y=y_j)P_Y(y_j), \hspace{10pt} \textrm{для любого множества $A$}.
\end{выравнивание}
Закон полного ожидания:
- Если $B_1, B_2, B_3,…$ является разбиением выборочного пространства $S$,
\begin{align}\label{eq:LOTPE-EV}
EX=\sum_{i} E[X|B_i]P(B_i) \hspace{57pt} (5.3)
\end{выравнивание} - Для случайной величины $X$ и дискретной случайной величины $Y$
\begin{align}\label{eq:LOTPE-RV}
EX=\sum_{y_j \in R_Y} E[X|Y=y_j]P_Y(y_j) \hspace{30pt} (5.4)
\end{выравнивание}
Пример
Пусть $X \sim Geometric(p)$. Найдите $EX$ по результату первого подбрасывания монеты.
- Раствор
- Помните, что случайный эксперимент $Geometric(p)$ заключается в том, что у нас есть монета с $P(H)=p$.
 Мы подбрасываем монету несколько раз, пока не увидим первый орёл. $X$ — общее количество подбрасываний монеты. Теперь есть два возможных исхода первого подбрасывания монеты: $H$ или $T$. Таким образом, мы можем использовать закон полного ожидания (уравнение 5.3):
Мы подбрасываем монету несколько раз, пока не увидим первый орёл. $X$ — общее количество подбрасываний монеты. Теперь есть два возможных исхода первого подбрасывания монеты: $H$ или $T$. Таким образом, мы можем использовать закон полного ожидания (уравнение 5.3):
\begin{выравнивание}%\метка{}
\номер EX &=E[X|H]P(H)+E[X|T]P(T)\\
\номер &=pE[X|H]+(1-p)E[X|T]\\
\номер &=p \cdot 1+(1-p)(EX+1).
\end{выравнивание}
В этом уравнении $E[X|T]=1+EX$, потому что броски независимы, поэтому, если первый бросок выпал решкой, это все равно, что начать заново при втором броске. Решая относительно $EX$, получаем
\begin{выравнивание}%\метка{}
\nonumber EX =\frac{1}{p}.
\end{выравнивание}
- Помните, что случайный эксперимент $Geometric(p)$ заключается в том, что у нас есть монета с $P(H)=p$.
Пример
Предположим, что количество клиентов, посещающих ресторан быстрого питания в данный день, равно $N \sim Poisson(\lambda)$. Предположим, что каждый покупатель покупает напиток с вероятностью $p$ независимо от других покупателей и независимо от стоимости $N$. {\infty} nP_N(n)=pE[N]=p\lambda.
{\infty} nP_N(n)=pE[N]=p\lambda.
\end{выравнивание}
/>
← предыдущая
следующая →
Печатная версия книги доступна на Amazon здесь.
|

 Мы подбрасываем монету несколько раз, пока не увидим первый орёл. $X$ — общее количество подбрасываний монеты. Теперь есть два возможных исхода первого подбрасывания монеты: $H$ или $T$. Таким образом, мы можем использовать закон полного ожидания (уравнение 5.3):
Мы подбрасываем монету несколько раз, пока не увидим первый орёл. $X$ — общее количество подбрасываний монеты. Теперь есть два возможных исхода первого подбрасывания монеты: $H$ или $T$. Таким образом, мы можем использовать закон полного ожидания (уравнение 5.3): Рассматриваемые темы: (1) подсчет количества возможных порядков, (2) подсчет с использованием правила умножения, (3) подсчет количества перестановок и (4) подсчет количества комбинаций.
Рассматриваемые темы: (1) подсчет количества возможных порядков, (2) подсчет с использованием правила умножения, (3) подсчет количества перестановок и (4) подсчет количества комбинаций.
 Сколько существует способов собрать две части? В таблице 2 перечислены все возможные варианты. Первым выбором может быть любой из четырех цветов. Для каждого из этих 4 первых вариантов есть 3 вторых варианта. Следовательно, есть 4 х 3 = 12 возможностей.
Сколько существует способов собрать две части? В таблице 2 перечислены все возможные варианты. Первым выбором может быть любой из четырех цветов. Для каждого из этих 4 первых вариантов есть 3 вторых варианта. Следовательно, есть 4 х 3 = 12 возможностей.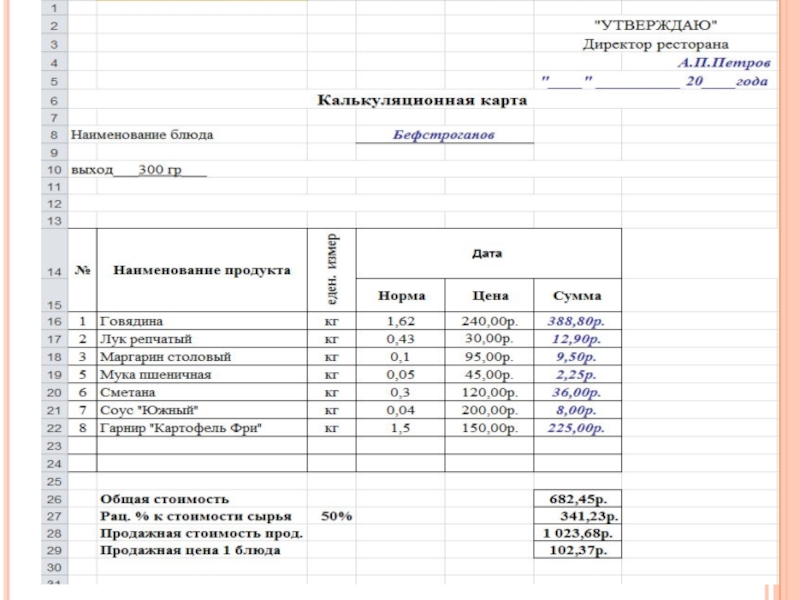 Общая формула:
Общая формула: В отличие от перестановок, порядок не учитывается. Таблица 3 основана на Таблице 2, но изменена таким образом, что повторяющимся комбинациям присваивается «x» вместо числа. Например, «желтый, затем красный» имеет «x», потому что комбинация красного и желтого уже была включена в качестве выбора номер 1. Как видите, существует шесть комбинаций трех цветов.
В отличие от перестановок, порядок не учитывается. Таблица 3 основана на Таблице 2, но изменена таким образом, что повторяющимся комбинациям присваивается «x» вместо числа. Например, «желтый, затем красный» имеет «x», потому что комбинация красного и желтого уже была включена в качестве выбора номер 1. Как видите, существует шесть комбинаций трех цветов.